cours Maple

INTRODUCTION A MAPLE

par

Nicolas CHIREUX

Remarque: ce cours fourni à mes élèves est basé sur la version 4 de Maple. La syntaxe de certaines fonctions a changé depuis; de nouvelles fonctions sont apparues. Mais dans l'ensemble, les données présentées ici restent valides.

Un version est téléchargeable au format acrobat (106K)

A)GENERALITES:

I) ARCHITECTURE GENERALE DE MAPLE:

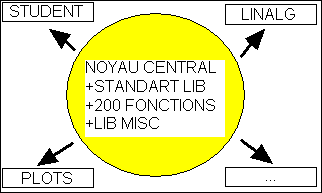
MAPLE est un logiciel de calcul formel fonctionnant autour d’un noyau central effectuant les calculs. Des bibliothèques contenant les fonctions les plus couramment utilisées sont ouvertes au démarrage.

Si l’on désire utiliser d’autres bibliothèques plus spécifiques, il faudra les charger préalablement par l’instruction:

with(nom de bibliothèque);

Maple possède 2500 fonctions intégrées recouvrant de nombreux domaines mathématiques.

L’aide -représentant de l’ordre de 500 pages- peut être appelée à tout moment de diverses manières:

-par la touche F1, on a accès au browser -”fouineur”-: par choix successifs de sujets de plus en plus précis,on arrive au sujet cherché. On l’utilise quand le nom de la fonction cherchée n’est pas connu.

-par ?nom de fonction, on accède directement aux pages d’aide concernant la fonction spécifiée.

II) FONCTIONNEMENT DE MAPLE:

1) généralités:

MAPLE travaille à partir du langage LISP - pour List Processing-. Il manipule donc des objets qui sont des listes:

-lors de l’entrée, l’utilisateur fournit une liste

-lors de l’évaluation, Maple modifie cette liste

-lors de l’affichage, Maple retourne à l’utilisateur la liste modifiée en guise de résultat.

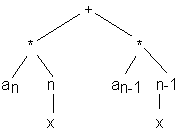
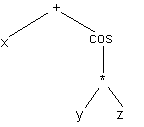
exemple d’entrée: l’expression x+cos(y*z); sera traduite sous la forme [opérateur,opérandes] soit [+,x,[cos,[*,y,z]]] afin d’être traitée.

On pourrait aussi choisir une représentation arborescente et visualiser l’expression par

exemple d’évaluation: pour évaluer la dérivée d’un produit D(f*g); Maple traduira l’expression par [D,[*,f,g]] puis va la transformer en: [+,[*,[D,f],g],[*,f,[D,g]]]

Si on choisit une représentation arborescente: 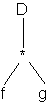sera transformé dans un premier temps en :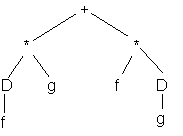

Le traitement de l’expression peut alors se poursuivre puisqu’on est ramené au calcul d’une dérivée simple.

2) aspect pratique:

On peut imaginer le fonctionnement de Maple comme une boucle sans fin:

-affichage du prompt >

-saisie d’une expression

-évaluation et simplification de l’expression

-affichage du résultat si la commande se termine par “;” ou non affichage si la commande se termine par “:”.

On parle de boucle TOP-LEVEL.

On peut taper plusieurs commandes à évaluer successivement sur un même ligne séparées par des “;” ou “:”.Les réponses seront affichées à la suite.

On peut écrire sur plusieurs lignes des instructions de commandes -si l’on souhaite par exemple écrire une procédure- sans évaluation intermédiaire en tapant “MAJ+ENTRÉE”.

Une même commande peut être découpée sur plusieurs lignes avec le “\”,les morceaux seront recollés par Maple avant évaluation - c’est juste un artifice de présentation.

On peut rappeler les trois dernières expressions évaluées -dans le déroulement chronologique- sans les retaper avec le “ pour la dernière,”” pour l’avant dernière et “”” pour l’antépénultième.

3) déroulement d’une évaluation:

Maple mémorise toutes les évaluations qu’il fait dans l’ordre chronologique. Cet ordre diffère parfois de l’ordre d’écriture.

exemple: >t:=5;

>t+4;

>t:=2;

Si on évalue la première expression puis ensuite la deuxième, Maple affiche 9 comme résultat. Évaluons ensuite la troisième expression puis à l’aide de la souris,on se repositionne sur la deuxième expression et on l’évalue à nouveau. Maple affichera alors 6 comme résultat!!

Il sera donc judicieux d’imposer un nettoyage de la mémoire centrale régulièrement: on le fait par l’instruction restart;.

On peut forcer Maple à évaluer une expression en l’analysant d’une façon déterminée par l’utilisateur. On utilise alors les instruction suivantes:

eval(expression)	est équivalent à ;
evalf(expression)	force l’utilisation de réels -float-
evalb(expression)	force l’utilisation de booléens
evalc(expression)	force l’utilisation de complexes
evalm(expression)	force l’utilisation de matrices

III) OBJETS MANIPULES PAR MAPLE:

1) les expressions:

L’expression est le type le plus général manipulé par Maple. Tout est une expression.

exemples: f:=x->x^3; b:=`pas de solution`; solve(x^3-4*x^2+1=0); ..

Comme vu précédemment, Maple traduira immédiatement ces expressions sous forme[opérateur,opérandes]. Il existe diverses fonctions permettant de visualiser cette traduction:

whattype(expression)	donne le type général (integer, float, complex, string, expseq, list, set, function, +, *, ^, =,...)
op(0,expression)	est plus précise que la précédente
op(expression)	donne la liste des opérandes
nops(expression)	donne le nombre des opérandes
op(i,expression)	donne la ième opérande
op(i..j,expression)	renvois la suite des opérandes du ième au jème

On peut modifier une expression à l’aide des fonctions suivantes:

map(f,expression)	où f est une fonction remplace chaque opérande de l’expression par f(opérande)
subs(s₁,...,s_n,expr)	où s₁,...,s_n sont des équations effectue les substitutions indiquées par les équations dans l’expression
subsop(i₁=e₁,...,i_n=e_n,e)	où les i_k sont des entiers remplace l’opérande de numéro i_k par l’expression e_kdans l’expression e
convert(expression,t)	remplace le type de l’expression par le nouveau type t sans changer les opérandes.

2) les séquences:

Une séquence - expseq - est une suite d’expressions séparées par des virgules. Elle n’est pas ordonnée,les diverses occurrences d’une valeur sont maintenues. Une séquence vide est notée NULL.

exemple: >1,2,6,5,4,5; sera évalué comme étant l’objet 1,2,6,5,4,5

On peut créer une séquence soit en la tapant directement soit par:

seq(f(i),i=m..n);	produisant la suite d’expressions f(m),f(m+1)...f(n)
seq(f(i),i=expression)	équivalent à seq(f(op( j,expression)), j=1.. nops(expression))

3) les listes:

Une liste - list - est une suite d’expressions séparées par des virgules et notées entre crochets [ ].Elle n’est pas ordonnée et les occurrences multiples d’une même valeur sont maintenues. Une liste vide est notée [ ].

exemple: >[1,2,6,5,4,5]; sera évaluée comme l’objet [1,2,6,5,4,5]

Pour ajouter un élément x à une liste l,on écrira: l:=[op(l),x];

Pour enlever le ième élément d’une liste l,on écrira: subsop(i=NULL,l)

4) les ensembles:

Un ensemble -set- ressemble à une liste si ce n’est qu’il est ordonné et que les occurrences multiples d’une même valeur sont supprimées. Il est noté entre accolades. Un ensemble vide est noté {}.

exemple: >{1,2,6,5,4,5}; sera évalué comme étant l’objet {1,2,4,5,6}

Pour ajouter un élément x à un ensemble e: e:=e union {x};

Pour enlever un élément x à un ensemble e: e:=e minus {x};

Pour calculer l’intersection de deux ensembles, on utilisera la fonction intersect

5) les tables et tableaux:

Une table est une application entre un ensemble d’indices et les valeurs qui y sont associées. Indices et valeurs peuvent être n’importe quelle expression. On crée une table par la fonction table:

t:=table() affecte à t une nouvelle table vide.

Pour accéder ou affecter une valeur à un élément d’une table, on utilise la notation t[indice]:

exemple: t[1]:=12; affecte à l’élément d’indice 1 la valeur 12. Si la table t n’avait pas été créée précédemment,elle l’est alors automatiquement.

exemple: notes[toto]:=12,3,7;

notes[alfred]:=1,6,14; crée une table notes et affecte à l’indice toto la séquence 12,3,7 et à l’indice alfred la séquence 1,6,14.

Attention!! l’évaluation du nom d’une table produit le nom de la table mais pas son contenu - ce n’est pas comme une variable assignée-.En effet,le nom de la table est un pointeur - sur une zone mémoire-,il ne représente donc pas le contenu. Il faudra imposer un eval(nom) pour que Maple retourne le contenu de la zone pointée.

Dans l’exemple ci-dessus >notes; renvoie notes alors que >eval(notes); renvois le contenu de la table notes.

Enfin deux fonctions utiles: indices(nom) renvois les indices de la table nom et entries(nom) renvoie les valeurs de la table nom.

Un tableau est une table particulière. Les indices seront forcément entiers et leurs bornes seront définies à la création du tableau: t:=array(1..n,1..m) crée un tableau à deux dimensions de bornes 1..n,1..m

6) les variables:

Pour Maple, une variable n’est pas typée. Elle peut se voir successivement affecter un entier, une expression,une chaîne...Une variable non initialisée reste une étiquette utilisable comme inconnue ou paramètre dans un calcul.

exemple: >x+4; retourne x+4

>x:=4;

>x+4; retourne 8

Pour évaluer une variable, Maple la remplace par sa définition,puis continue ainsi récursivement pour les variable apparaissant dans cette définition etc...

eval(variable)	évalue complètement la variable
eval(i,variable)	évalue la variable au ième niveau.

Pour empêcher l’évaluation d’une variable, il faut la mettre entre guillemets simples ‘.

B) MANIPULATION DES NOMBRES SOUS MAPLE:

I) GENERALITES:

1) type:

Tout nombre (RÉEL, ENTIER, RATIONNEL) peut être:

positive >0

negative <0

nonneg >=0

On peut tester le signe par type(r, positive) ou is(r, positive) par exemple.

2) restriction du champ de la variable:

assume(x,prop)	prop est une propriété
is(x,prop)	teste si x a la propriété prop
isgiven(x,prop)	teste si la propriété prop a été donnée à x
about(x)	retourne les propriétés de x
additionally(x,prop)	ajoute une propriété à x

Pour faire cesser la restriction,il faut affecter la variable - x:=3 par exemple- ou la désaffecter x:=’x’.

II) LES ENTIERS:

1) type:

Ce sont des objets de type integer pouvant être:

posint >0

negint <0

nonnegint >=0

even pair

odd impair

primeint premier

Ce type peut être testé:

is(n,positive); is(4,negint); type(12,even);

2) changement de base de numération:

La fonction convert permet avec l’option base de changer de base de numération:

convert(entier,base,b)	convertit l’entier de la base 10 vers la base b.Le retour se fait de la forme: entier=[a₀,a₁,...] qu’il faut lire a₀b⁰+a₁b¹+..
convert(entier,base,b1,b2)	convertit l’entier de la base b1 vers la base b2
convert(entier,option)	on l’utilise pour les conversions du système décimal vers les bases 2 (binaire),8 (octal),16(hexadécimal) avec les options binary,octal,hex.

3) fonctions usuelles:

abs(n)	retourne la valeur absolue de n
factorial(n) ou n!	retourne la factorielle de n
ifactor(n)	décompose n en facteurs premiers
ifactors(n)	donne la liste des facteurs premiers de n. Il faut préalablement lire la bibliothèque ifactors par readlib(ifactors)
type(n,facint)	teste si n a été décomposé en facteurs premiers
igcd(n₁,n₂,...)	retourne le pgcd des nombres
ilcm(n1,n2,..)	retourne le ppcm des nombres
iquo(a,b,’r’)	retourne le quotient de la division de a par b. ’r’ est optionnel et contient le reste de la division.
irem(a,b,’q’)	retourne le reste de la division de a par b. ’q’ est optionnel et contient le quotient de la division.
isprime(n)	retourne TRUE si n est premier
ithprime(n)	retourne le nième nombre premier,le premier étant 2
nextprime(n)	retourne le plus petit nombre premier strictement supérieur à n
min(n₁,n₂,...)	retourne le plus petit des nombres de la liste
rand()	retourne un entier positif aléatoire de 12 chiffres
sign(n)	retourne -1 si n<0, 1 sinon
isolve(éq,vars)	résout dans l’ensemble des entiers l’équation(ou le système d’équations) éq, vars est optionnel est la (ou les) variable suivant laquelle se fait la résolution. Si vars est absent,les variables sont notées_N1,_N2...

III)LES RATIONNELS:

1) type: fraction ou rational

Le type peut être testé par type(q,fraction); ou type(q,fraction(nonneg));

2) fonctions usuelles:

numer(q)	isole le numérateur
denom(q)	isole le dénominateur
ifactor(q)	factorise le numérateur et le dénominateur
is(q,facint)	teste la décomposition de q
abs,max et min	comme les entiers

Il existe d’autres fonctions portant sur les rationnels. Elles sont dans la librairie numtheory. Il faut l’ouvrir par with(numtheory);.

Pour avoir la liste de ces fonctions, il suffit de taper ?numtheory

IV) LES REELS ET COMLEXES:

1) type:

float pour réel ou complex pour complexes

écriture: mantisse*10^exposantou Float(mantisse,exposant)

La partie entière et décimale de la mantisse sont séparées par un point. Le type peut être testé par type ou is.

2) constantes prédéfiniées:

E base des logarithmes naturels

Pi pour le nombre pi. Attention à la majuscule!!

infinity pour +∞

-infinity pour -∞

Les constantes de Maple ne sont pas vues comme étant du type float mais du type string ou encore chaînes de caractères.

3) précision:

Maple est très performant dans les calculs numériques mais connaît les mêmes problèmes d’approximation que les autres outils numériques. Par exemple, Maple ne retourne pas z=0 dans l’exemple suivant:

On peut par contre demander le calcul littéral par simplify(x/y) ou simplify(z) qui donnent 1 et 0.

4) fonctions usuelles:

pour avoir une liste ?inifcns

op(r)	retourne deux entiers,la mantisse et l’exposant du réel r
Digits:=n	fixe à n le nombre de décimales dans les calculs. n=10 par défaut
evalf(expr,d)	force le calcul numérique de expr avec d décimales. Si d est omis c’est Digits qui controle.
Re(z), Im(z)	partie réelle,imaginaire de z
evalc(z)	simplifie l’écriture d’un complexe
round(r)	entier le plus proche de r- si r=a+Ib, round(a)+Iround(b)
ceil(r)	plus petit entier >=r - même remarque si r est complexe
floor(r)	plus grand entier <=r - même remarque si r est complexe
trunc(r)	troncature -même remarque si r est complexe
abs(z)	valeur absolue si z est réel, module si z est complexe
argument(z)	argument de z
conjugate(z)	conjugué de z

La plupart des fonctions mathématiques peuvent être utilisées avec les complexes: exp, ln, log, log[b], sin, cos, sinh, cosh, tan, tanh, cot, coth, arccos, arcsin, arctan, arccosh, arcsinh, arctanh, arccot, arccoth, sec, sech, csc, csch, arcsc, arccsch, arcsec, arcsech

5) transformation des expressions:

Maple permet de transformer toutes les fonctions - simplifier, regrouper, factoriser, développer...-. Les méthodes sont nombreuses.

combine(expr,noms)	transforme l’expression expr en un seul terme. Noms est optionnel choisi parmi: exp, trig,power, Psi, ln
convert(expr,forme)	transforme une liste en somme,produit, ensemble, tableau, un ensemble en liste, un tableau en liste, en liste de listes. Pour résumer, cette fonction convertit une expression en une autre de nature différente. Pour l’aide, ?convert
expand(expr,ex1,...exn)	développe expr en préservant les expression optionnelles ex1,...exn
factor(expr)	factorise expr
normal(expr)	simplifications de base et factorisations simples sur expr
radsimp(expr)	simplifie une expression contenant des radicaux
simplify(expr,n₁,...n_k)	simplifie expr,les arguments n_i sont optionnels
collect(xpr,v,forme,f)	ordonne xpr comme un polynôme en la variable v ,forme (option) est recursive(par défaut) ou distributed. f (option) est appliquée à tous les coefficients

C) LES POLYNOMES:

I MANIPULATION DE POLYNOMES:

1) Généralités:

Les polynômes sont des expressions que Maple stocke comme les autres. On peut les représenter sous forme d’arbre avec les additions au niveau supérieur puis aux niveaux inférieurs les multiplications et puissances.

On peut isoler des opérandes en utilisant les fonctions op(p) ou op(i,p) déjà vues.

Maple développe toutefois des fonctions spécifiques aux polynômes qui vont nous en faciliter le traitement.

Maple travaille avec les polynômes de plusieurs variables ce qui imposera de spécifier la variable suivant laquelle on appliquera la fonction.

2) manipulation de termes:

coeff(p,x,n)	retourne le coefficient de x^n si le polynôme est ordonné.
coeffs(p,x,’t’)	construit une séquence avec tous les coefficients. ’t’ est optionnel. Maple lui affecte les x^i dans le même ordre que les coefficients de la séquence. Intéressant si certains coefficients sont nuls
lcoeff(p,x,’t’)	renvoie le coefficient de plus haut degré en x
tcoeff(p,x,’t’)	renvoie le coefficient de plus bas degré. ’t’ est optionnel dans ces deux fonctions
degree(p,x)	renvoie le degré en x du polynôme
ldegree(p,x)	renvoie le plus bas degré du polynôme

3) regroupement de termes:

collect(a,x,g,f)	groupe les coefficients de même degré en x. g et f sont optionnels. Noter l’option distributed pour les polynômes à plusieurs variables.
normal(p)	présente p sous forme classique
sort(p,options)	ordonne un polynôme en respectant les options s’il y en a.
expand(p)	développe p par distribution des produits sur les sommes
convert(p,horner)	factorise p sous forme d’un polynôme de Horner
compoly(r,x)	retourne p(x) et x=q(x) tels que subs(x=q(x),p(x))=r(x). Il faut pour l’utiliser lire la bibliothèque compoly par readlib(compoly);

II) OPERATIONS ARITHMETIQUES:

1) opérations classiques:

+,-,*,^	addition, soustraction, multiplication et puissance
quo(a,b,x,’r’)	calcule le quotient de a par b,le reste est stocké dans r
rem(a,b,x,’q’)	calcule le reste de la division de a par b,le quotient est stocké dans q
gcd(a,b,’cofa’,’cofb’)	calcule le pgcd de a et b, cofa et cofb sont optionnels:ce sont les cofacteurs cofa=a/gcd(a,b)
lcm(a,b)	calcule le ppcm de a et b.
content(a,x,’pp’)	calcule le pgcd des coefficients de a.pp vaut a/pgcd(coeff)
primpart(p,x)	donne le résultat de p/content(p,x) comme le pp précédent
divide(a,b,’q’)	retourne TRUE si la division de a par b est exacte en stockant le quotient dans q, FALSE si la division n’est pas exacte, q n’est alors pas affecté

2) divers:

subs(x=expression,p)	substitue expression à x dans le polynôme p. On peut s’en servir pour évaluer p en une valeur de x donnée.
norm(p,n)	calcule la norme d’ordre n du polynôme à savoir la racine nième de la somme des coefficients de p à la puissance n.
powmod(a,n,b,x)	retourne a^n mod b
randpoly	génère un polynôme aléatoire
interp(x,y,v)	retourne le polynôme d’interpolation e Lagrange du nuage de points dont les coordonnées sont dans x et y sous forme de liste

III) RACINES D’UN POLYNOME ET FACTORISATION:

MAPLE dispose de diverses fonctions pour trouver les racines d’un polynôme. Le choix sera guidé par la forme souhaitée pour les résultats.

realroot(p,taille)	isole des intervalles de la largeur de taille contenant chacun une racine. Il faut au préalable lire la bibliothèque realroot par readlib(realroot);
roots(p,options)	cherche les racines exactes du polynôme. Maple retourne les racines sous la forme [valeur,multiplicité]. Si le champ n’est pas spécifié, Maple cherche les racines dans l’ensemble auquel appartiennent les coefficients du polynôme. On peut étendre ce champ ou en spécifier un autre en ajoutant des options.
fsolve(p,var,options)	retourne une approximation réelle ou complexe des racines. Le champ de recherche est fixé par les coefficients du polynôme.On peut forcer une résolution en complexe par l’option complex. On peut limiter le domaine de recherche en spécifiant borne-inf..borne-sup en guise d’option On peut aussi ne faire rechercher qu’un certain nombre de racines par l’option maxsols=nombre.
irreduc(p,options)	teste l’irréductibilité d’un polynôme sur le champ fixé par les coefficients du polynôme. On peut étendre ce champ ou en spécifier un autre en ajoutant des options
factor(p,options)	factorise un polynôme

D) LES FONCTIONS

I DEFINITION:

1) les méthodes de définition:

-par la flèche: f:=var->expr.

S’il y a plusieurs variables: f:=(var1,var2,...)->expr;

-par les procédures: f:=proc(var)...end; .

S’il y a plusieurs variables: f:=proc(var1,var2...)...end;

-grâce à une expression déjà calculée: unapply(expr,var1,var2...) renvoie la fonction (var1,var2...)->expr

Le résultat de la fonction peut être autre chose qu’un nombre, par exemple une liste de nombre - c’est à dire un vecteur-: f:=(var1,var2...)->[expr1,expr2,...]

2) domaines de définition, de continuité:

Les deux fonctions suivantes sont à charger dans le noyau central par readlib avant emploi. Elles sont à manier avec précaution,le problème de la continuité étant difficile à résoudre en informatique.

singular(fonct,var)	permet de déterminer les singularités d’une fonction
iscont(fonct,x=a..b,’closed’)	permet d’étudier la continuité de la fonction sur l’intervalle [a,b]- fermé avec l’option closed- ou ]a,b[ -sans l’option closed-

3) image d’intervalle,extréma:

Les fonctions evalr, minimize et extrema sont à utiliser après chargement par readlib.

evalr(fonction([a,b]))	détermine l’image de l’intervalle [a,b] par fonction
minimize(fonction,{vars},intervalle)	retourne le minimum de fonction par rapport à la variable vars dans intervalle
maximize(fonction,{vars},intervalle)	idem pour le maximum
extrema(fonction,{contraintes},var,’s’)	donne les extrema de fonction par rapport à var en tenant compte des contraintes - s’il n’y a pas de contraintes,écrire {}-. Les valeurs correspondantes de var sont stockées dans s

II) ETUDES LOCALES:

1) limites:

limit(fonct,x=a,dir)	recherche une limite à fonct en a -valeur, infinity,-infinity - dans la direction dir - left,right, real, complex -
Limit(fonct,x=a,dir)	forme inerte.Maple écrit la limite sans la calculer - traitement de texte -.La fonction value permet de forcer le calcul des formes inertes

2) développement en séries:

taylor(expr,x=a,n)	developpement en série de expr en x=a -valeur, infinity , -infinity,0 par défaut - à l’ordre n -6 par défaut
series(expr,x=a,n)	même chose mais en plus général
asumpt(expr,x)	même chose mais seulement en +infini à l’ordre 6
coeftayl(expr,x,n)	donne le coefficient du terme à la puissance 10 dans la série sans la calculer
series(leadterm(expr),x=a,n)	terme principal du développement en série de expr en x=a à l’ordre n - 6 par défaut -
convert(ser,polynom)	transforme la série ser en polynôme
mtaylor(expr,v,n)	développe en série à l’ordre n - 6 par défaut l’expression à plusieurs variables expr aux points donnés par la liste des variables v

III) DERIVEES,INTEGRALES:

1) dérivée:

diff(a,x1,x2...xn)	dérivée de l’expression ou fonction a par rapport aux variables x1,x2...xn successivement
diff(a,x$n)	dérivée d’ordre n de a par rapport à x.$ est appelé opérateur séquentiel
Diff(a,x1,x2...xn)	Diff est la forme inerte -traitement de texte-. Pour forcer le calcul,on utilise value

2) opérateur différentiel:

D(f)	dérivée de f -fonction d’une seule variable-. C’est équivalent à D(f)=unapply(diff (f(x),x),x)
D[i$n](f)	dérivée n^ième de f par rapport à la i^ème variable
D[i,j](f)	dérivée de f par rapport à la i^ème variable,puis à la j^ème variable
(D@@n)(f)	dérivée n^ième de f -fonction d’une seule variable-

3) intégrales:

int(f,x)	retourne la primitive de f.Maple n’affiche pas la constante d’intégration. Int en est la forme inerte
int(f,x=a..b,options)	intégrale définie de f entre a et b
changevar(chang,int,u)	faire with(Student) avant. Effectue le changement de variable dans l’intégrale int,chang est de la forme f(x)=g(u) où x est l’ancienne variable et u la nouvelle.
intparts(int,u)	faire with(student) avant. Fais l’intégration par parties,u étant le facteur à dériver dans int.

E) RESOLUTION D’EQUATIONS

I RESOLUTION D’EQUATIONS:

1) instruction de base:

-solve(eqns,vars) où eqns est une équation et vars la variable.Maple cherche une solution formelle de l’équation sur le champ associé aux coefficients -rationnels...-.Si aucune solution n’est trouvée,Maple retourne la valeur NULL.

Rem 1: Si à la place d’une équation,on entre une expression dans eqns,Maple va résoudre expr=0 par défaut.

Rem 2: Si aucune variable n’est entrée dans vars,Maple résoudra sur toutes les variables apparaissant dans l’équation eqns.

Rem 3: Parfois,Maple retourne la ou les solutions en utilisant la fonction RootOf(fonction(_Z)) dans le but de simplifier l’affichage.On peut toutefois forcer le calcul fonction(_Z)=0 par allvalues(RootOf(...)).

Rem 4: pour résoudre un système d’équations,on entrera le système sous forme d’un ensemble {eqn1,eqn2...} dans eqns et les variables sous forme d’un ensemble {var1,var2...} dans vars.

Rem 5: eqns peut être une inéquation.Le retour se fera sous la forme d’une inégalité:par exemple var1>val1

Rem 6: eqns peut avoir pour variable une fonction f(x).Maple retournera alors une procédure proc(x) ...end permettant de calculer la fonction f solution de l’équation eqns.

Rem 7: solve(identity(eqn,x),vars) permet de résoudre l’équation eqn vérifiée quelque soit x sur les variables vars

Rem 8: solve(series(f(x),x)=y,x) force la résolution de l’équation f(x)=y sous la forme d’un développement en série à l’ordre 6 par défaut.On peut fixer préalablement l’ordre par Order=n.Le retour est donné sous forme d’une série en y.Si on remplace dans f(x) la variable x par ce développement,on obtient y.

Rem 9: pour les systèmes linéaires,on peut utiliser les matrices pour la résolution sous la forme AX=B où A est la matrice des coefficients,X le vecteur des inconnues et B le vecteur second membre.

2) résolution numérique:

On peut forcer Maple à résoudre numériquement avec l’instruction solve vue précédemment en entrant des coefficient réels dans l’équation eqns: par exemple solve(x^2-3*x+1) retournera (3+sqrt(5))/2... alors que solve(x^2-3*x+1.0) retournera 2.6180033...

Maple dispose toutefois de fonctions plus évoluées:

fsolve(eqns,vars,opts)	retourne la valeur numérique des solutions sur le champ de recherche fixé par les coefficients.Il existe 3 options utiles: complex pour forcer le calcul en complexes,maxsols=n pour fixer le nombre maximum de solutions à retourner et val1..val2 pour limiter l’intervalle de recherche
isolve(eqns,vars)	permet de forcer la résolution sur les entiers
msolve(eqns,vars,m)	permet de forcer la résolution sur Z/mZ

3) résolution de récurrences:

Maple dispose d’une fonction spécifique à la résolution d’équation impliquant des récurrences:

rsolve(eqns,fonct,opt) où eqns est la (ou les) relation de de récurrences et fonct représente la fonction vérifiant la récurrence. Si l’on désire fournir les premiers éléments de la suite -u₀,u₁...-on écrit alors {relation1, relation2..., terme0=val0, terme1=val1...} à la place d’eqns. Si aucune valeur initiale n’est fournie,Maple les remplacera par fonct(0),fonct(1)...

Pour les suites récurrentes linéaires,l’option ‘genfunc’(x) permet d’obtenir la fonction génératrice de la suite. Cette fonction est où u_n est le terme général de la suite vérifiant la relation de récurrence eqns.y vérifie aussi la relation de récurence!

II) RESOLUTION D’EQUATIONS DIFFERENTIELLES:

1) instruction de base:

dsolve(eqns,vars,options) effectue la résolution de l’équation différentielle eqns suivant la variable vars.

Rem 1: s’il y a des conditions initiales,elles doivent être fournies en même temps que l’équation différentielle sous forme d’un ensemble {equa diff,cond initiale}.

Rem 2: eqns peut être un système d’équations différentielles.

Parmi les options,on notera:

-type=nom où nom peut être exact - par défaut, le résultat est alors formel -, numeric - le résultat est alors une procédure qu’on peut appeler pour diverses valeurs numériques- ou series - le résultat est alors donné sous forme d’un développement en série.

-method=nom2 où nom2 peut être rkf45 - par défaut,résolution par la méthode de Range Kutta d’ordre 4 ou 5- ,dverk78 - résolution par la méthode de Range Kutta d’ordre 7 ou 8- ou laplace - résolution par la méthode de Laplace qui autorise l’utilisation de fonctions de Dirac ou Heavyside -.

-explicit=val où val est false - par défaut - ou true - dans ce cas,on force Maple à donner le résultat explicitement en fonction de la variable dépendante...mais ce n’est pas toujours possible!!-

-value=array([val1,val2...]) retourne un tableau à deux lignes:la première contient le nom des valeurs calculées - x,y(x),y’(x)-,la deuxième contient une matrice constituée de chacune des valeurs val1,val2... et de l’ évaluation de la solution de l’équation différentielle en ces points.

F) ALGEBRE LINEAIRE

I LES MATRICES:

1) Généralités:

C’est le package linalg qui contient les diverses fonctions nécessaires aux manipulations et calculs concernant les matrices.Une matrice diffère d’un tableau par ses indices qui sont forcément entiers et strictement positifs - pas d’indice 0!-.

Une matrice se déclare par matrix(n,p,[[a₁₁,...,a_1p],...,[a_n1,...,a_np]]) où n et p sont les nombres de lignes et de colonnes - optionnels - et [[a₁₁,...,a_1p],..., [a_n1,...,a_np]] les coefficients de la matrice.Certains coefficients peuvent rester indéterminés.

2) Matrices particulières:

band(b,n)	crée une matrice bande à partir du vecteur b
diag(B₁,B₂,...B_n)	construit une matrice en plaçant les matrices B₁,B₂...B_n sur la diagonale.On dit que la matrice générée est diagonale par blocs. C’est équivalent à BlockDiagonal(B₁,B₂,...B_n)
genmatrix(eqns,vars)	génère une matrice à partir des coefficients des variables vars dans le système d’équations linéaires eqns
hilbert(n,x)	crée une matrice de Hilbert de dimension nxn telle que les coefficients a_ij=1/(i+j-x). x=1 par défaut
jacobian(f,v)	calcule la matrice jacobienne du vecteur f par rapport aux coordonnées stockées dans le vecteur v. On a:
randmatrix(m,n)	crée une matrice aléatoire de dimension mxn
toeplitz(L)	crée une matrice de Toeplitz à partir de la liste L. Maple place L₁ sur la diagonale, puis L₂ sur la ligne immédiatement au dessus puis celle au dessous et ainsi de suite
vandermonde(L)	crée une matrice de Vandermonde:a_i1=1 et si j≠1
Wronskian(f,v)	crée la matrice wronskienne du vecteur f par rapport à la variable v: a_1j=f_jet si i≠1

3) Manipulations:

augment(A,B,...)	crée une matrice en joignant horizontalement les matrices A,B,..... C’est équivalent à concat(A,B,...)
row(A,i)	extrait la ligne i de la matrice A
row(A,i..k)	extrait les lignes i à k de la matrice A
col(A,i)	extrait la colonne i de la matrice A
col(A,i..k)	extrait les colonnes i à k de la matrice A
delrows(A,r..s)	supprime les lignes r à s de la matrice A
delcols(A,r..s)	supprime les colonnes r à s de la matrice A
copyinto(A,B,m,n)	copie la matrice A dans la matrice B en plaçant l’élément A₁₁en B_mn et ainsi de suite
extend(A,m,n,x)	ajoute m lignes et n colonnes initialisées à x à la matrice A
minor(A,r,c)	supprime la ligne r et la colonne c de la matrice A
submatrix(A,i..j,k..t)	extrait la sous matrice de A constituée par les lignes i à j et les colonnes k à t
swapcol(A,c₁,c₂)	permute les colonnes c₁ et c₂
swaprow(A,r₁,r₂)	permute les lignes r₁ et r₂

4) Tests sur les matrices:

coldim(A)	retourne le nombre de colonnes de A
rowdim(A)	retourne le nombre de lignes de A
equal(A,B)	retourne TRUE si A_ij=B_ij pour tous i et j
iszero(A)	retourne TRUE si A_ij=0 pour tous i et j
colspace(A,'dim')	retourne une base de l’espace vectoriel engendré par les vecteurs colonnes de la matrice. Dim est optionnel et contient la dimension de cet espace vectoriel
rowspace(A,'dim')	retourne une base de l’espace vectoriel engendré par les vecteurs lignes de la matrice. Dim est optionnel et contient la dimension de cet espace vectoriel
kernel(A,'nulldim')	retourne une base du noyau de l’application linéaire représentée par la matrice A. Nulldim est optionnel et contient la dimension du noyau. C’est équivalent à nullspace(A)
orthog(A)	retourne TRUE si A est une matrice orthogonale à savoir A est constitué de vecteurs colonnes de norme 1 et orthogonaux entre eux
rank(A)	retourne le rang de la matrice A
trace(A)	retourne la trace de la matrice A

5) Opérations sur les matrices:

add(A,B,c₁,c₂)	calcule c₁A+c₂B.Si c₁ et c₂ sont égaux à 1,on peut les omettre. C’est équivalent à evalm(A+B)
multiply(A,B,...)	multiplie les matrices A,B,... entre elles
exponential(A,t)	retourne la matrice
addrow(A,r₁,r₂,m)	crée une matrice A’ où la ligne r₂ est remplacée par m*row(A,r₁)+row(A,r₂)
addcol(A,c₁,c₂,m)	crée une matrice A’ où la colonne c₂ est remplacée par m*col(A,c₁)+col(A,c₂)
mulrow(A,r,expr)	multiplie la ligne r de la matrice A par expr
mulcol(A,c,expr)	multiplie la colonne c de la matrice A par expr
adjoint(A)	retourne la matrice adjointe de A.Elle est telle que A.A^†=det(A)I où I est la matrice identité. C’est équivalent à adj*(A)
htranspose(A)	retourne la matrice A’ telle que
transpose(A)	retourne la matrice A’ telle que
det(A)	calcule le déterminant de la matrice A
inverse(A)	calcule l’inverse de la matrice carrée A
norm(A,opt)	calcule la norme de la matrice A suivant l’option spécifiée
charmat(A,lambda)	retourne la matrice caractéristique M de A.Elle est telle que M=lambdaI-A.Rem: det(M) donne le polynôme caractéristique. C’est équivalent à charpoly*(A,lambda)
eigenvals(A)	donne les valeurs propres de la matrice A.Ce sont aussi les solutions du polynôme caractéristique précédent
eigenvects(A)	retourne les vecteurs propres de la matrice A sous la forme [[val. prop. i, multiplicité,{vect[1,i],...vect[n_i,i]}]...] où vect[j,i] est un vecteur propre associé à la valeur propre i et n_i est la dimension du sous espace propre de cette valeur propre - n_i< multiplicité!!
pivot(A,i,j)	effectue un pivot de Gauss en prenant A_ij pour pivot.Maple annule donc tous les A_kj avec k≠i.
ffgausselim(A,'r','d')	effectue un pivot de Gauss sur la matrice A sans faire apparaître de fractions.Le résultat est une matrice triangulaire supérieure. r contient le rang de A et d son déterminant - ils sont optionnels -
gausselim(A,'r','d')	même fonction mais les fractions sont autorisées
gaussjord(A,'r','d')	fait apparaître des 1 ou 0 sur la diagonale.r contient le rang de A et d son déterminant - ils sont optionnels -
jordan(A)	retourne la forme de Jordan de la matrice A à savoir une matrice diagonale dont la diagonale est constituée par les valeurs propres de A
linsolve(A,B)	si B est un vecteur,Maple retourne le vecteur x solution de A.x=B. Si B est une matrice,Maple retourne la matrice X solution de A.X=B

II) LES vecteurs:

1) Généralités:

C’est le package linalg qui contient les diverses fonctions nécessaires aux manipulations et calculs concernant les vecteurs.

Un vecteur se déclare par vector(n,[a₁,a₂,...a_n]) où n est la dimension - optionnelle- et [a₁,a₂,...a_n] les composantes du vecteur dont certaines peuvent être indéterminées si l’utilisateur ne fait pas d’entrée les concernant.

Même si Maple affiche les vecteurs en ligne,ce sont des vecteurs colonnes et il seront traités comme tels.Un vecteur ligne devra être entré comme une matrice à une seule ligne.

2) Opérations sur les vecteurs:

angle(u,v)	retourne l’angle en radians entre les vecteurs u et v
basis(v)	trouve une vase de l’espace vectoriel engendré par l’ensemble de vecteurs v
GramSchmidt(v)	transforme un ensemble v de vecteurs linéairement indépendants en un ensemble de vecteurs orthogonaux deux à deux
dotprod(u,v,'orthogonal')	produit scalaire de u par v
crossprod(u,v)	produit vectoriel de u par v
norm(v)	calcule la norme du vecteur - possibilité d’options-
normalize(A)	rend le vecteur v unitaire
randvector(m)	génère un vecteur de dimension m à éléments aléatoires
subvector(v,i..j)	crée un sous-vecteur de v en extrayant les éléments i à j
vectdim(v)	retourne la dimension du vecteur v

3) Opérateurs:

grad(expr,v,coords=type)	calcule le gradient de l’expression expr par rapport aux composantes du vecteur v dans le système de coordonnées spécifié par type
laplacian(expr,v,coords=type)	calcule le laplacien de l’expression expr par rapport aux composantes du vecteur v dans le système de coordonnées spécifié par type
vectpotent(f,v,'V')	retourne TRUE si le vecteur f est le rotationnel d’un potentiel vecteur V pour les coordonnées contenues dans le vecteur v
potential(f,v,'F')	retourne TRUE si le vecteur f est le gradient d’un potentiel scalaire F pour les coordonnées contenues dans le vecteur v

G) LE GRAPHISME

I) GRAPHISME EN 2D:

1) Les options:

On peut affecter à la majorité des fonctions graphiques une série d’options aux effets divers. Au cours des exemples choisis pour illustrer les fonctions,on utilisera la majorité d’entre elles. La syntaxe est simple:les options s’écrivent à la suite des paramètres fondamentaux de chaque fonction en les séparant par des virgules.

ex: fonction(paramètres,option1=valeurs1,option2=valeur2...);

Aucune des options n’est obligatoire car Maple affecte une valeur par défaut à chacune d’elles.

Les options les plus importantes sont les suivantes:

-scaling: contrôle de l’échelle du graphe.Si CONSTRAINED est choisi,tout changement d’échelle affecte également x et y contrairement à UNCONSTRAINED. La valeur par défaut est UNCONSTRAINED.

-axes: choix du type d’axes.FRAME:axes sur le bord;BOXED:axes entourant le graphe; NORMAL:axes se croisant en zéro;NONE:pas d’axes.

-coords=polar: choix des coordonnées polaires.La première coordonnée est le rayon,la seconde est l’angle.Aucun nom n’est imposé.

-numpoints=n: nombre de points minimum généré lors de l’appel à la fonction (par défaut n=49).Maple choisit automatiquement d’en générer plus quand la fonction n’est pas régulière.

-resolution=n: choix de la résolution horizontale de l’écran en pixels (par défaut n= 200).

-color=n: choix de la couleur.n peut être un nom parmi les suivants:

aquamarine,black,blue,navy,coral,cyan,brown,gold,green,gray,grey,khaki,magenta, maroon,orange,pink,plum,red,sienna,tan,turquoise,violet,wheat,white,yellow.

n peut aussi être soit COLOUR(RGB,a,b,c) soit COLOUR(HUE,d) où a,b,c,d sont compris entre 0 et 1.

-xtickmarks=n: nombre minimum de graduations sur l’axe des x.Il existe la même option pour l’axe y:c’est ytickmarks=n.

-style=s: style du dessin (par défaut LINE).Avec POINT,dessin constitué de points,

avec LINE,dessin linéaire,avec PATCH,taches de couleurs pour les polygones.

-discont=s: si s à la valeur TRUE,Maple analyse la fonction pour trouver ses discontinuités et faire ensuite un graphe propre.Par défaut,s est FALSE.

-title=t: titre du dessin.s est une chaîne de caractères entre ‘’.

-thickness=n: épaisseur des lignes du tracé, n vaut 0, 1, 2, ou 3.0 est l’épaisseur par défaut.

-linestyle=n: style des lignes.Si n=0 tracé plein.

-symbol=s: choix de la forme des points lors d’un tracé par points parmi BOX, CROSS, CIRCLE,POINT, et DIAMOND.La valeur par défaut est POINT.

-view=[xmin..xmax,ymin..ymax]: choix de la partie de la courbe affichée.Par défaut la courbe entière est affichée.

2) Les fonctions:

a) tracé d’une courbe:

La syntaxe est : plot(fonction,h,v,options);

-h est le domaine horizontal de la forme var=valeur1..valeur2 ou simplement valeur1..valeur2 si la variable est évidente.h est obligatoire

-v est la domaine vertical d’affichage:il est optionnel.Par défaut,toute la courbe est affichée.

-options:ce sont les options définies au 1).Aucune n’est obligatoire.

Pour la fonction,diverses possibilités sont offertes:

-la fonction simple: plot(tan(x),x=-2*Pi..2*Pi,y=-4..4, discont=true);

Noter l’option et la majuscule à Pi!

La fonction peut aussi être un opérateur: plot(cos + sin, 0..Pi);

On peut retracer la fonction avec d’autres paramètres à l’aide de l’instruction replot.

p := plot(sin(x),x=0..2*Pi):

-la fonction paramétrique: elle est notée entre crochets [x(t),y(t),t=val1..val2]

plot([sin(t), cos(t), t=-Pi..Pi]);

-la fonction en coordonnées polaires: c’est un cas particulier des fonctions paramétriques. L’option coords=polar impose un tracé en coordonnées polaires

plot([cos(5*t),t,t=0..2*Pi],coords=polar);

plot([x^2,x,x=0..3*Pi],-8..8,-10..10,coords=polar);

Noter la différence entre domaine de variation du paramètre entre[] et domaine d’affichage.

-l’ensemble de fonctions: si on veut tracer plusieurs fonctions sur un même graphe,il faut les noter entre accolades.

plot({sin(x), x-x^3/6}, x=0..2);

plot({x,[x^2,x,x=-1..1]},x=0..1); noter ici que,si parmi les fonctions il y a une fonction paramétrique,on doit utiliser pour les autres le nom du paramètre comme variable.

-la fonction à domaine de variation infini: le domaine -∞,+∞ est transformé en -1,1 par approximation de la fonction arctan:le tracé sera en conséquence déformé au voisinage de l’infini.

plot(sin(x), x=0..infinity);

plot( {exp,ln}, -infinity..infinity );

-la fonction procédure: la fonction peut être une procédure qu’on repère par son nom.

w:=proc(x) if x<0 then -x elif (x>0) and (x<4) then x else -x+8 fi end;

plot(w,-5..6);

-l’ensemble de points: une ensemble de points est noté [[x1,y1],[x2,y2],...].

l := [[0,0],[1,1],[2,1]];

plot(l, x=0..2, style=point,symbol=diamond); noter les options et essayer d’en changer (style=line...)

-le fonction complexe: on trace par conformal les images d’une grille par la fonction complexe définie.Le pas de la grille est fixé par défaut (11 lignes) et modifiable par grid=[n1,n2].Le nombre de points évalués sur chaque ligne de la grille est fixé par numxy=[n1,n2] ou par défaut (15 points).

conformal(1/z,z=-1-I..1+I,-6-6*I..6+6*I);

conformal(cos(z),z=0..2*Pi+ Pi*I,grid=[8,8],numxy=[11,11]);

conformal(z^3,z=0..2+2*I,xtickmarks=3,ytickmarks=6); noter ici les options.

-le champ de vecteurs: il est noté [f(x,y),g(x,y)].Maple trace par fieldplot un vecteur évalué en x,y de direction et de norme fixée par f et g.

fieldplot( [x/(x^2+y^2+4)^(1/2),-y/(x^2+y^2+4)^(1/2)],x=-2..2,y=-2..2);

fieldplot([y,-sin(x)-y/10],x=-10..10,y=-10..10,arrows=LINE, color = x); changer les options (style des flêches arrows=LINE,SLIM,THIN ou THICK)

-le champ de gradient: Maple trace par la fonction gradplot un champ de vecteurs dérivant d’un potentiel donné.

gradplot(x^2+2*y^2+1,x=-1..1,y=-1..1,grid=[15,15], color = x^2+2*y^2+1); noter la valeur de l’option COLOR.

-la fonction implicite: on utilise la fonction implicitplot pour tracer une fonction définie de manière implicite (équation,procédure...).Par défaut,la fonction est évaluée en 625 points (25 sur x et 25 sur y dans les domaines définis.

p:= proc(x,y) if x^2 < y then x^2 + y^2 else x - y fi end:

implicitplot(p,-2..2,-1..3);

b) les tracés particuliers:

-le tracé semi-logarithmique: seule l’échelle sur l’axe y est logarithmique.

logplot(x->10^x,1..10);

logplot({ x->2^(sin(x)), x->2^(cos(x))}, 1..10);

-le tracé logarithmique:les deux échelles sont logarithmiques.

loglogplot(10^x,x=1..10);

loglogplot([1,2,3,4,5,6,7,8],style=POINT);

loglogplot([[1,2],[3,4],[5,6],[7,8]]);

-le tracé de densité: il permet par la fonction densityplot le tracé d’une fonction 3D en 2D.Plus la valeur de la fonction au point x,y est élevée,plus le tracé est foncé.

densityplot(sin(x*y),x=-Pi..Pi,y=-Pi..Pi,axes=boxed);

-le tracé retardé: tout tracé est une structure à laquelle on peut affecter un nom.Si on écrit variable=plot(...),le tracé est calculé mais pas affiché.Il est stocké dans variable.Pour l’afficher ensuite,il y a deux possibilités:soit variable; soit display(variable,options); .L’avantage de display est qu’il permet une affichage multiple.

F:=plot(cos(x),x=-Pi..Pi,y=-Pi..Pi,style=line):

G:=plot(tan(x),x=-Pi..Pi,y=-Pi..Pi,style=point):

display({F,G},axes=boxed,scaling=constrained,title=`Cosine and Tangent`);

-l’affichage de texte: la syntaxe est textplot([x,y,`texte`],options);.Maple affiche le texte au point x,y.Il y a de nombreuses options sur le texte.On retiendra seulement celle d’alignement:align=ABOVE,RIGHT,LEFT,BELLOW.

p := plot(sin(x),x=-Pi..Pi):

delta := 0.05:

t1 := textplot([Pi/2,1+delta,`Local Maxima (Pi/2, 1)`],align=ABOVE):

t2 := textplot([-Pi/2,-1,`Local Minima (-Pi/2, -1)`],align=BELOW):

display({p,t1,t2});

-le tracé de polygones: polygonplot trace un polygone à partir de la séquence des coordonnées de ses sommets.

ngon := n -> [seq([ cos(2*Pi*i/n), sin(2*Pi*i/n) ], i = 1..n)]:

display([ polygonplot(ngon(8)), textplot([0,0,`Octagon`]) ], color=BLUE); tester l’option patch

-le tracé de matrice: en 2D,le tracé se limite à un tracé de contenu.Maple affiche par la fonction sparsematrix un point en x (indice de ligne) et y (indice de colonne) si l’élément de matrice est non-nul.

with(linalg):

A := randmatrix(15,15,sparse):

B := gausselim(A):

PA := sparsematrixplot(A, color=green):

PB := sparsematrixplot(B, color=red):

display({PA, PB}); changer la forme des points

c) les animations:

Il est possible de créer des animations de courbes par la fonction animate.L’option frames=n fixe le nombre d’images de l’animation (par défaut 16);l’option numpoints=m fixe le nombre de points de chaque image.

animate( sin(x*t),x=-10..10,t=1..2,frames=50);

animate( {x-x^3/u,sin(u*x)}, x=0..Pi/2,u=1..16 ,color= red);

animate( [u*t,t,t=1..8*Pi], u=1..4,coords=polar,frames=60,numpoints=100);

On peut stocker une animation dans une variable pour affichage ultérieur.

P := animate(sin(x+t),x=-Pi..Pi,t=-Pi..Pi,frames=8):

Q := animate(cos(x+t),x=-Pi..Pi,t=-Pi..Pi,frames=8):

display([P,Q]); essayer l’option insequence=true.Elle permet d’enchainer des animations les unes après les autres.Par défaut insequence=false,chaque image est alors la superposition des fonctions.

II) GRAPHISME EN 3D:

1) Les options:

Les options du graphisme en 2D sont toujours valable ici mais s’y ajoutent un lot d’options spécifiques au graphisme en 3D.Nous ne citerons que les principales.

-grid=[m,n]:choix du maillage sur lequel sont évalués les points.

-style=s:choix du mode de dessin de la surface.s est POINT, HIDDEN (parties cachées non représentées), PATCH, WIREFRAME (maillage uniquement représenté), CONTOUR lignes de niveau), PATCHNOGRID (combinaison de styles), PATCHCONTOUR (combinaison de styles), ou LINE.la valeur par défaut est HIDDEN.

-contours = n:choix du nombre de lignes de niveau.n est un entier positif (10 par défaut).

-coords=c: choix du système de coordonnées parmi cartesian,spherical et cylindrical.La valeur par défaut est cartesian.

-projection=r:choix de la perspective,r doit être compris entre 0 et 1.r=0 correspond à une vue grand angle,r=1 correspond à une projection orthogonale,r=0.5 correspond à la projection normale (valeur par défaut:1).

-orientation=[theta,phi]:choix du point de vue sous forme des deux angles sphériques theta et phi anglo-saxons (noms inverse des nôtres).Par défaut les deux angles valent 45°

-shading=s:choix du mode de colorisation de la surface.s est soit XYZ, XY, Z, Z_GREYSCALE, Z_HUE, NONE.

-ambientlight=[r,g,b]:définition de la lumière d’ambiance dans laquelle baigne le dessin.r,g,b (pour red,green,blue) sont compris entre 0 et 1.

-light=[phi,theta,r,g,b]:choix de l’éclairage du dessin.la source éclaire sous les angles theta et phi avec une lumière dont la couleur est fixée par les valeurs de r,g,et b.

2) Les fonctions:

a) tracé d’une courbe:

La syntaxe est : plot3d(fonction,hx,hy,options);

-hx est le domaine de variation de x de la forme var=valeur1..valeur2 ou simplement valeur1..valeur2 si la variable est évidente.hx est obligatoire

-hy est le domaine de variation de y de la forme var=valeur1..valeur2 ou simplement valeur1..valeur2 si la variable est évidente.hy est obligatoire

-options:ce sont les options définies au 1) plus celles du graphisme 2D.Aucune n’est obligatoire.

En graphisme 3D,il y a souvent plusieurs possibilités pour obtenir un même tracé:soit par plot3d avec choix d’option soit par le fonction dédiée.Dans la suite,chaque fois que la fonction dédiée existe,elle est présentée avec son homologue plot3d.

Pour la fonction,diverses possibilités sont offertes:

-la fonction simple: plot3d(sin(x)/x*sin(y)/y,x=-2*Pi..2*Pi,y=-2*Pi..2*Pi);

Noter l’influence des styles et du mode de colorisation.

-la fonction paramétrique: elle est notée entre crochets [x(t),y(t),t=val1..val2]

plot3d([x*sin(x)*cos(y),x*cos(x)*cos(y),x*sin(y)],x=0..2*Pi,y=0..Pi);

On peut aussi tracer une courbe en coordonnées paramétriques par spacecurve([fonction],domaine);

spacecurve([cos(t),sin(t),t],t=0..4*Pi);

spacecurve({[sin(t),0,cos(t),t=0..2*Pi],[cos(t)+1,sin(t),0,numpoints=10]},

t=-Pi..Pi,axes=FRAME);

-la fonction en coordonnées cylindriques: L’option coords=cylindrical impose un tracé en coordonnées cylindriques.On fournit la fonction sous la forme r(theta,z) ou en paramétriques [f(theta,z),g(theta,z),h(theta,z)].

plot3d(theta*z/5,theta=0..6*Pi,z=-5..5,coords=cylindrical);

plot3d([x*u,u,x*cos(u)],x=-8..8,u=0..4*Pi,coords=cylindrical);

On peut aussi utiliser la fonction cylinderplot(fonction,domaine theta,domaine.z,options); où domaine.theta est le domaine de variation de theta et domaine.z celui de z.

cylinderplot(z+ 3*cos(2*theta),theta=0..Pi,z=0..3);

cylinderplot([z*theta,theta,cos(z^2)],theta=0..Pi,z=-2..2, color = theta);

-la fonction en coordonnées sphériques: L’option coords=spherical impose un tracé en coordonnées sphériques.On fournit la fonction sous la forme r(theta,phi) ou en paramétriques [f(theta,phi),g(theta,phi),h(theta,phi)].

plot3d((1.3)^x * sin(y),x=-1..2*Pi,y=0..Pi,coords=spherical,style=patch);

plot3d([z*theta,exp(theta/10),z^2],theta=0..Pi,z=-2..2,coords=spherical);

On peut aussi utiliser la fonction sphereplot(fonction,domaine.phi,domaine theta,options); où domaine.phi est le domaine de variation de phi et domaine.theta celui de theta.

sphereplot((1.3)^z * sin(theta),z=-1..2*Pi,theta=0..Pi,style=patch,color=z);

-l’ensemble de fonctions: si on veut tracer plusieurs fonctions sur un même graphe,il faut les noter entre accolades.

c1:= [cos(x)-2*cos(0.4*y),sin(x)-2*sin(0.4*y),y]:

c2:= [cos(x)+2*cos(0.4*y),sin(x)+2*sin(0.4*y),y]:

c3:= [cos(x)+2*sin(0.4*y),sin(x)-2*cos(0.4*y),y]:

c4:= [cos(x)-2*sin(0.4*y),sin(x)+2*cos(0.4*y),y]:

plot3d({c1,c2,c3,c4},x=0..2*Pi,y=0..10,grid=[25,15],style=patch,color=sin(x));

-la fonction procédure: la fonction peut être une procédure qu’on repère par son nom.

p:= proc(x,y) if x^2 < y then cos(x*y) else x*sin(x*y) fi end:

h:= proc(x) x^2 end:

plot3d(p,-2..2,-1..h); noter que le domaine de variation d’une variable peut dépendre de l’autre y compris par l’intermédiaire d’une procédure.

-l’ensemble de points: une ensemble de points est noté de deux manières:soit [x1,y1,x2,y2,...] soit [[x1,y1],[x2,y2],...].On peut le représenter par plotpoint(liste,options);

points:= { seq([cos(Pi*T/40),sin(Pi*T/40),T/40],T=0..40) }:

pointplot(points);

On peut aussi tracer une surface à partir de points par la fonction surfdata(liste,options);

cosdata := [seq([ seq([i,j,evalf(cos((i+j)/5))], i=-5..5)], j=-5..5)]:

sindata := [seq([ seq([i,j,evalf(sin((i+j)/5))], i=-5..5)], j=-5..5)]:

surfdata( {sindata,cosdata}, axes=frame, labels=[x,y,z] ,style=patch);

-le champ de vecteurs: il est noté [f(x,y,z),g(x,y,z),h(x,y,z)].Maple trace grâce à fiedplot3d(fonction,domainex,domainey,domainez,options); un vecteur évalué en x,y,z de direction et de norme fixée par f,g et h.

fieldplot3d([2*x,2*y,1],x=-1..1,y=-1..1,z=-1..1,grid=[5,5,5]);

-le champ de gradient: Maple trace grâce à gradplot3d(fonction,domainex, domainey,domainez,options); un champ de vecteurs dérivant d’un potentiel donné.

gradplot3d( (x^2+y^2+z^2+1)^(1/2),x=-2..2,y=-2..2,z=-2..2);

-la fonction implicite: on utilise la fonction dédiée implicitplot3d(fonction,

domainex,domainey,domainez,options); pour tracer une fonction définie de manière implicite (équation,procédure...).Par défaut,la fonction est évaluée en 1000 points (10 sur x,10 sur y et 10 sur z dans les domaines définis.

implicitplot3d( x^3 + y^3 + z^3 + 1 = (x + y + z + 1)^3,x=-2..2,y=-2..2,z=-2..2, grid=[13,13,13]);

b) les tracés particuliers:

-le tracé de niveau: par la fonction contourplot(fonction,domainex,domainey,

options); Maple génère un tracé en lignes de niveau de la fonction 3D.

contourplot((1.3)^x * sin(y),x=-1..2*Pi,y=0..Pi,coords=spherical); changer le point de vue à la souris.

contourplot(sin(x*y),x=-Pi..Pi,y=-x..x);

-le tracé de tubes: par la fonction tubeplot([courbe paramétrée,domaine, radius=n],options); Maple génère un tube de rayon radius sur la base de la courbe paramétrée donnée.

tubeplot({[cos(t),sin(t),0,t=Pi..2*Pi,numpoints=15,radius=0.25*(t-Pi)],

[0,cos(t)-1,sin(t),t=0..2*Pi,numpoints=45,radius=0.25]});

-le tracé retardé: tout tracé est une structure à laquelle on peut affecter un nom.Si on écrit variable=plot3d(...),le tracé est calculé mais pas affiché.Il est stocké dans variable.Pour l’afficher ensuite,il y a deux possibilités:soit variable; soit display3d(variable,options); .L’avantage de display3d est qu’il permet une affichage multiple comme son pendant en graphisme 2D.

F:=plot3d(sin(x*y),x=-Pi..Pi,y=-Pi..Pi):

G:=plot3d(x + y,x=-Pi..Pi,y=-Pi..Pi):

H:=plot3d([2*sin(t)*cos(s),2*cos(t)*cos(s),2*sin(s)],s=0..Pi,t=-Pi..Pi):

display3d({F,G,H});

-l’affichage de texte: la syntaxe est textplot3d([x,y,z,`texte`],options);. Maple affiche le texte au point x,y.Il y a de nombreuses options sur le texte.On retiendra seulement celle d’alignement:align=ABOVE,RIGHT,LEFT,BELLOW.

-le tracé de polygones: polygonplot3d trace un polygone à partir de la séquence des coordonnées de ses sommets.

list_polys := [seq([seq([T/10,S/20,sin(T*S/20)],T=0..20)],S=0..10)]:

polygonplot3d(list_polys,style=patch,axes=boxed);

-le tracé de matrice: en 3D,la fonction matrixplot trace le contenu d’une matrice.Maple affiche un point en x (indice de ligne) et y (indice de colonne) dont la côte z a pour valeur celle de l’élément de matrice correspondant.

with(linalg):

A:= hilbert(8):

B:= toeplitz([1,2,3,4,-4,-3,-2,-1]):

matrixplot(A+B,heights=histogram,axes=frame,gap=0.25,style=patch);

c) les animations:

Il est possible de créer des animations de courbes par animate3d.L’option frame=n fixe le nombre d’images de l’animation (par défaut 8);l’option numpoints=m fixe le nombre de points de chaque image.

animate3d((1.3)^x * sin(u*y),x=-1..2*Pi,y=0..Pi,u=1..8,coords=spherical);

animate3d(sin(x)*cos(t*u),x=1..3,t=1..4,u=1/4..7/2,coords=cylindrical);

III) LES EQUATIONS DIFFERENTIELLES:

1) tracé simple:

Maple peut tracer directement la solution d’une équation différentielle par odeplot.Cette fonction fait partie de la bibliothèque (plots).

Il faut une résolution numérique préalable.Dans l’exemple qui suit p est la procédure de résolution numérique créée par Maple à l’appel de dsolve.

sys := diff(y(x),x)=z(x),diff(z(x),x)=y(x):

fcns := {y(x), z(x)}:

p:= dsolve({sys,y(0)=0,z(0)=1},fcns,type=numeric):

odeplot(p, [x,y(x)], -4..4, numpoints=25);

odeplot(p, [[x,y(x)],[x,z(x)]],-4..4,numpoints=25);

odeplot(p, [y(x),z(x)],-4..4,numpoints=25); diagramme de phase

odeplot(p, [x,y(x),z(x)],-4..4,numpoints=25, color=orange); diagramme en 3D ,chaque point étant défini paramétriquement.

2) la bibliothèque DEtools:

Maple dispose d’une bibliothèque dédiée au tracé de solutions d’équations différentielles ou de système d’équations différentielles.On l’appelle par with(DEtools):

a) la fonction DEplot:

Son rôle est le tracé soit de solutions d’équations différentielles d’ordre n du type diff(y(x),x$n)=f(x,y) où f(x,y) peut contenir des dérivées de y,soit de système de deux équations différentielles d’ordre 1 du type :x’=f(t,x,y) y’=g(t,x,y).

La syntaxe est la suivante:DEplot(diffeq,vars,domaine.t,cond.init.,options);

-diffeq:équations à résoudre.Si le système est linéaire,on peut se contenter d’entrer la matrice des coefficients (V’=M.V où V=[x,y])

-vars:spécification des variables dans l’ordre variable indépendante puis variables dépendantes [t,x,y] ou [x(t),y(t)] par exemple.Si le système admet une solution explicite y(x),il vaut mieux entrer la variables sous la forme [x,y] (accélération de la résolution).

-domaine.t:domaine de variation de la variable indépendante

-cond.init.:ce sont les conditions initiales sous la forme [t0,x0,y0] ou [x(t0)=x0,

y(t0)=y0].Si un jeu de conditions est donné,Maple trace une solution par condition.Par défaut,les conditions initiales sont prises nulles.

-options:il y en a de nombreuses.Les plus importantes sont:stepsize=h qui fixe le pas d’intégration (domaine/20 par défaut),method=nom où nom est euler,backeuler,impeuler ou rk4 (par défaut rk4 pour Range Kutta d’ordre 4) qui fixe la méthode d’intégration.

with(DEtools):

A := linalg[matrix](2,2,[a,b,c,d]):

a := 0: b := -2: c := 1: d := -2:

DEplot(A, [x,y], -10..10, {[0,0,2],[0,0,4],[0,-6,0],[0,-4,0],[0,0,-2],[0,0,-4],[0,6

,0],[0,4,0]}, stepsize=.2, scene=[x,y], x=-10..10, y=-10..10, title=`spiral sink`);

DEplot([y,-sin(x)-y/10],[t,x,y],-10..10,{[0,1,1]},stepsize=.5);

DEplot([y,-sin(x)-y/10],[x,y],-10..10,{[0,1,1]}); noter la différence de résultat suivant le choix des variables.

a1 := diff(y(x),x$4)+2*diff(y(x),x$2) -cos(x)=3;

DEplot(a1,[x,y],0..2,{[1,1,2,3,0]});

b) la fonction DEplot1:

Son rôle est de tracer les solutions d’équations différentielles d’ordre 1 du type y’=f(t,y).Sa syntaxe est DEplot1(équadiff,vars,domaine.t,cond.init.,domaine.y,options);

Elle se présente comme la fonction précédente.Ne citons que les différences:

-domaine.y:on peut en option limiter le domaine de variation de la variable dépendante.

-options:il y a ici une option supplémentaire: limitrange=true ou false qui impose l’arrêt de l’intégration lorsqu’on sort du domaine fixé pour y.

DEplot1(diff(y(t),t)=sin(t-y), y(t), t=-Pi..Pi, y=-Pi..Pi);

DEplot1(x*(1-x),[t,x],t=0..10, {[0,.5],[0,.25],[0,.1],[0,1],[0,2]}, x=0..2);

c) la fonction dfieldplot:

Cette fonction recouvre partiellement ce que fait DEplot2.En effet,elle fournit la cartographie sous forme de vecteurs de dy/dx où y et x sont obtenus par résolution d’un système différentiel d’ordre 1 ou par une équation différentielle d’ordre 1.La syntaxe est dfieldplot(équations,vars,domaine.t,options);

A:=[x*(1-y),.3*y*(x-1)]:

dfieldplot(A,[x,y],-2..2,x=-1..2,y=-1..2,arrows=THICK,title=`Lotka-Volterra model`);

d) la fonction phaseportrait:

Cette fonction recouvre aussi partiellement l’action de DEplot2. En effet,étant donné un système de deux équations différentielles d’ordre 1, elle fournit la tracé de y(x) ou à défaut le tracé en 3D de x(t) et y(t).

La syntaxe est phaseportrait(équations,vars,domaine.t,cond.init.,options);

A:=[x*(1-y),.3*y*(x-1)]:

phaseportrait(A,[x,y],-7..7,{[0,1.2,1.2],[0,1,.7]},stepsize=.2,title=`Lotka-Volterra model`);